On this page we will explore some of the physics of the didgeridoo and answer these questions:

1. How long do I have to cut a (PVC) pipe to get a certain musical key?
2. Which musical key will I get if I play on a pipe of a certain length.

This page is written using some material kindly supplied by Wolfgang Droescher (click here for Wolfgang's original article).

First of all lets be clear no amount of physics will be able to describe a termite hollowed didgeridoo. Termite hollowed didgeridoos have a very irregular inner surface unique to each didgeridoo which do give many a genuine didgeridoo very interesting sound characteristics, but make it far too complicated to describe physically.

So for the purpose of this page we need to reduce a didgeridoo to a perfect pipe. Consequently this page is really about the physics of a PVC didgeridoo or any other didgeridoo as long as the inside diameter is exactly the same for the whole length of the didgeridoo.

Next lets have a look at some basic music theory:

• Each musical note is defined by it's frequency.
• International tuning in music is based on middle A with a frequency of exactly 440 Hz (Hertz)
• On a standard scale we have 12 notes in a full octave: c, c#, d, d#, e, f, f#, g, g#, a, a#, b, (c)
• Due to the nature of sound waves the increase of frequency between two steps is not linear, but logarithmical. In plain words: the change of frequency cannot be described as "frequency of c plus increase factor equals frequency of c#", but as "frequency of c multiplied by increase factor equals frequency of c#"
• The frequency doubles on every octave, i.e. a' = 440 Hz, a'' = 880 Hz
• Resulting from the two latter points we have an increase factor of the 12th root of 2 between any two musical keys (12 steps make 2 times the basic frequency) = 1.05946

Now that we have covered a bit of basic music theory lets see what actually influences f- the frequency a given pipe resonates at:

• c - The speed of sound, which is 344 m/s in dry air at a temperature of 20° C (or 355 m/s in dry air of +40° C)
• l - The length of the pipe

Note: The diameter of the pipe is not important at all for this basic calculation; a bigger diameter only makes the pipe sound louder as it gives a higher amplitude.

Which leads us finally to the physics formula determining the frequency a certain didgeridoo resonates at (as long as it is a perfect pipe):

• f = c / 4l (Reads: The frequency (f) equals the speed of sound (c) divided by four times the length (l) of the open pipe)
• Or, the other way round: l = c / 4f (The length (l) equals the speed of sound (c) divided by four times the frequency (f) )

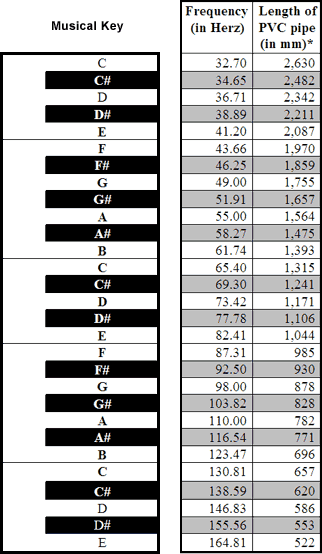
Using this formula we have prepared this table that gives you both the frequency of a particular key as well as the length of a PVC didgeridoo in that key.

Let's say you want to build a PVC didge with a musical key of C (as described on How to make a didge for less than 10$).

We need (apart from the hardware) the formula from above, the frequency table on left - and a calculator.

l = c / 4f = 344 / (4 x 65.40) = 344 / 261.63 = 1.315 m

That's it!

The other way round: Let's assume you found a wonderful hollowed branch (which is a perfect pipe) of roughly one meter in length out in your backyard and you are wondering which musical key this "didge" would make. After smoothing the edges a bit you end up with exactly 1.05 m. Take out your calculator and start off:

f = c / 4l = 344 / (4 x 1.05) = 344 / 4.2 = 81.90 Hz

This is pretty close to E (82.41Hz), so now you have a rough idea which key you can make out of it. Use the formula above to get the exact length for E (1.04 m) then cut off some more millimetres - done! Or simply leave your new didge as is, it's close enough anyway.

As we stated earlier our calculations are based on the speed of sound in dry air at 20° C. So what happens if it gets hotter or colder, or wetter?

We will ignore humidity here as there is no easy formula to account for it and the speed of sound in air depends mostly on temperature; it can be calculated with this small formula:

c = 331.6 + 0.6 x t
with c = speed of sound in m/s
and t = air temperature in °C

Examples:
at 0° C you get c = 331.6 + 0.6 x 0 = 331.6 m/s
at 10° C you get c = 331.6 + 0.6 x 10 = 337.6 m/s
at 20° C you get c = 331.6 + 0.6 x 20 = 343.6 m/s
at 30° C you get c = 331.6 + 0.6 x 30 = 349.6 m/s
at 40° C you get c = 331.6 + 0.6 x 40 = 355.6 m/s

This means that the frequency of a 1.32cm long didgeridoo will be about 3.4% higher if the temperature is 40° C, which is halfway between C and C#.

As you can see extreme temperature changes will change the key of your didj, but a few degrees warmer or colder than 20° C do not matter much. Wolfgang also reminded me that we are talking about the temperature of the air going through the didj which is your breath. And that does not change that much.

Keep on didjing...

Read on:
Physics of the Didgeridoo - End Correction
In Depth Physics of the Didgeridoo
Australian Aboriginal Musical Instruments - The Didjeridu, The Bullroarer And The Gumleaf
The Physics of Dreamtime: An analysis of the acoustical properties of a didgeridoo
Vocal Tract Resonances and the Sound of the Australian Didjeridu (Yidaki)
What Makes a Good Didj?