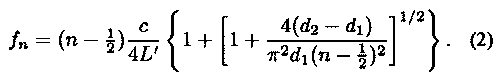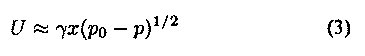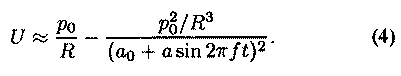1. INTRODUCTION
The didjeridu (commonly spelt didgeridoo) or yiraki of the Australian aboriginal people is a very ancient instrument with considerable
acoustic interest, despite its extremely simple construction. It consists of a more-or-less straight piece of tree trunk or branch, hollowed
out by the successive action of fire and termites to produce a gently flaring tube. Didjeridus from Central Australia are typically about one
metre in length, while those from Arnhem Land are usually about 1.5 metres long. The longer didjeridus are now generally preferred because they
allow a greater range of musical effects. In each case the blowing end is about 30 mm in internal diameter and the free end about 50 mm, though
all these dimensions vary significantly from one instrument to another, even among those by the same maker. The average wall thickness is usually
5 to 10 mm. At the blowing end, the walls are coated with a rim of resinous gum, to improve playing comfort, and the free end is often given
a slight extra flare by internal scraping. The outside of the instrument is smoothed and painted in geometrical totemic designs, usually in black,
white and orange.
To play the didjeridu, the musician seals the narrow end of the tube around his mouth, blows, and vibrates his lips under muscular
tension in very much the same way as used in playing a brass instrument such as the tuba. The didjeridu uses air at rather a high rate so that,
to playa sustained tone, the player adopts the technique of "circular breathing". After playing normally for a few seconds, he expands his cheeks
with air, seals off his mouth from his throat with the back of the tongue and, while using the stored air to maintain the tone, takes a quick
breath through his nose. This technique is common on certain other instruments, such as Indonesian flutes, and is now used routinely by oboists
and even flute players to play without breath breaks for as long as several minutes. In these instruments, with their much smaller breath demand,
the objective is to maintain an even tone and cover up any effect of the breathing. With the didjeridu, however, the player makes a virtue of
necessity and emphasises the rhythmic breathing cycle to produce a pulsating drone. The pulsations are usually further decorated by tongue vibrations,
so that the player effectively says unvoiced words such as "ritoru" or even "didjeridu", with the final "u" sound prolonged. The westernised
name "didjeridu" for the instrument perhaps arises from this circumstance, though it may perhaps be a word from some aboriginal language, now
extinct.
There has been only a little written about the acoustics of the didjeridu [1,2] or about its playing techniques [3,4]. The instrument itself, however, has become increasingly used in popular music by groups
such as Gondwanaland, and was earlier made widely known on television through the efforts of Rolf Harris. A few simple calculations and measurements,
however, allow us to understand a good deal about this interesting instrument.
2. PASSIVE ACOUSTICS
It is a good approximation to treat the didjeridu as a truncated conical horn of length L. Suppose that the diameter
of the smaller end is d1 and that of the larger end d2. Then if we imagine the cone to be continued to its
apex, the distance from this apex to the smaller blowing end of the instrument will be x1 = d1L/(d2 - d1).
Since the players' lips form a pressure-controlled valve, the preferred sounding frequencies are those at which the acoustic pressure at this
end, and thus the acoustic impedance, is a maximum. These frequencies fn can be shown [5] to
be the roots of the equation
where kn = 2pifn/ c, c is the speed of sound in air, and the acoustic length L' = L + 0.3d2 includes
the end-correction at the open end.
If the flare is extremely small so that the horn is nearly cylindrical, then x1 becomes very large and tan-1knpi
approaches pi/2. The resonance frequencies are then fn = (n - ½)c/2L' which form the series of odd harmonics that we
expect, for example as the playing frequencies of a clarinet, starting with a quarter of a wavelength equal to the tube length. More generally,
if the flare is fairly small, we can expand the result (1) to arrive at the approximate expression
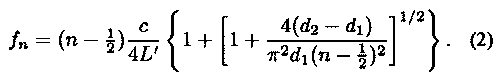 We can see that the frequencies of the lower modes, and particularly that of the fundamental, are raised relatively more than those of the
higher partials, so that all the mode intervals are compressed. For moderate flare, only the lowest mode frequency is significantly affected.
For the range of end diameters found in the typical didjeridus of Table 1, this fundamental-mode frequency is raised by a factor between about
1.06 and 1.38 relative to a cylindrical tube of the same length. The ratio of second to first mode frequencies, which would be a perfect twelfth
(1.50) for a cylindrical pipe, ranges from about 1.30 (about a tone flat of a perfect twelfth) to about 1.43 (a little less than a semitone flat).
The greater the flare, the flatter the second mode appears relative to the drone fundamental.
TABLE 1. Typical didjeridus [1]
| Length L (cm) |
159 |
144 |
149 |
| Diameter d1 (mm) |
31 |
26 |
30 |
| Diameter d2 (mm) |
36 |
60 |
40 |
| Frequency f1 (Hz) |
60 |
80 |
64 |
| Drone pitch |
B1 |
E2 |
C2 |
These mode-frequency predictions are confirmed by the measured drone frequencies of three typical didjeridus from Arnhem Land
as listed in Table 1. The effect of flare is easily seen in the case of the second and third instruments - the second is only 3 percent shorter
than the third, but its fundamental frequency is 25 percent higher because of its large flare. Unfortunately the second-mode frequencies were
not recorded, but the pitches agree qualitatively with the theoretical predictions [1].
It is interesting to note that traditional makers and players seem to have little concern with either the drone frequency or
the interval to the second mode - the first two instruments in the table are actually by the same maker. Indeed, a good player can produce most
of the nuances of traditional performances on a piece of plastic pipe of appropriate diameter and length! When used in popular Western music,
however, it is necessary to select a didjeridu of appropriate pitch to match the keyboard instruments, though in some multi-track recordings
the didjeridu is actually recorded first and then pitch-shifted, the player having made some adjustment for the associated change in tempo. Breaking
with tradition, Graham Wiggins has made the perhaps obvious extension of building a didjeridu with keys to open one or more holes near the foot
and so allow the drone pitch to be changed.
3. SOUNDING MECHANISM
While much of our understanding of the sounding mechanism of wind instruments dates back to the time of Helmholtz a hundred
years ago [6], it is only recently that these mechanisms have been studied in
detail. There is a clear distinction between three types of pressure-controlled valves, as illustrated in Fig. 1. In the first two types, air
pressures acting on the two faces of the valve have opposite effects, tending to either open or close the valve, while in the third type excess
pressure on either face tends to open the valve. If we represent a closing action of excess pressure by the symbol - and an opening action by
+ , then the first two valves have classification ( -, + ) and ( +, - ) respectively, and the third has classification ( +, + ).
The familiar reed valves of oboes and clarinets are of the ( - , + ) type, as also are the metal reeds used in organ reed-pipes.
The human vocal folds are usually modelled as having the configuration ( +, + ), as are the vocal organs of birds (the syrinx), though the models
used are generally more complex than this. The lips of players of brass instruments, such as the trumpet or tuba, and of the didjeridu, are either
of configuration ( +, - ) or ( +, + ), and possibly change character between different playing regimes [7] . It is probably necessary to use a rather complex model for the vibrating lip valve, such
as has been developed for the human vocal folds [8], but this has not yet been attempted. We must therefore be satisfied for the present with
simpler models.
If we define the acoustic admittance of a pressure-controlled valve under blowing pressure, as viewed from the instrument, to
be the ratio of the small-signal acoustic flow out of the instrument to the small-signal acoustic pressure in the instrument mouthpiece, then
there is the possibility of self -sustained oscillation if the resistive part of this impedance (the acoustic conductance) is negative, to overcome
the losses in the system, and if the reactive part can be balanced by the reactive admittance of the instrument tube and the players mouth, taken
together. In all cases, the first condition requires that the blowing pressure should be greater than some threshold value determined by the
tension of the lip muscles, which itself depends on the pitch of the note being played [9,10].
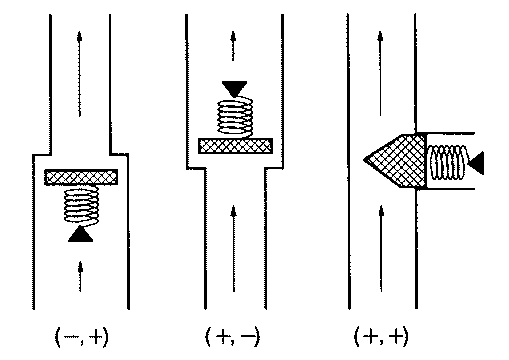
Figure 1. The three types of simple pressure-controlled valve. Air flow direction is shown with an arrow.
Provided a blowing pressure greater than this minimum is used, then the acoustic admittance of a lip-valve generator can be
shown [9] to have a form like one of those shown in Fig. 2. For such a ( +, - ) or a ( +, + ) valve,
the acoustic conductance - the real part of the admittance - is large and negative at a frequency either just above or just below the resonance
frequency of the lip-valve, which is determined by lip mass and muscular tension. At other frequencies the conductance is relatively small and
may be either positive or negative. The magnitude of this peak negative conductance is sufficiently large that it is able to overcome the positive
conductance losses in the rest of the system and force it into oscillation. While this can happen over a considerable frequency range if the
lip resonance frequency is adjusted - a skilled trombone player can play a glissando without moving the instrument slide-the oscillation is most
easily sustained near an impedance maximum of the tube, where its positive conductance is least. The acoustic impedance of the player's mouth
also plays an important role in sustaining the lip oscillation - a role that can be appreciated when we realise that it is possible to buzz the
lips at their resonance frequency even in the absence of any instrument tube [10].
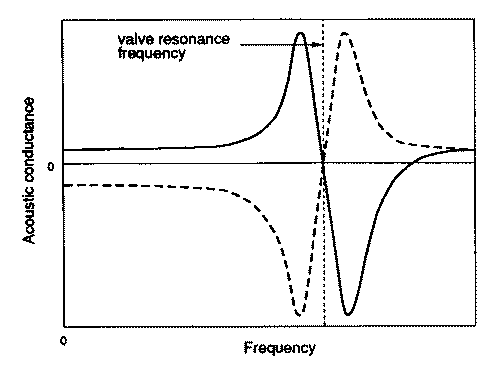
Figure 2. Acoustic conductance of a ( +, - ) valve (full line) and of a ( +, + ) valve (broken line).
The resonance frequency for free vibration of the valve is shown.
This is the operating regime for a didjeridu-the player adjusts lip tension so that the lip resonance is close to the first
tube resonance. To produce the second mode, the player must use a much higher lip tension to raise the lip resonance frequency, and this requires,
in turn, a greater threshold blowing pressure. The actual pressures used are, of course, well above the threshold value. Measurements [1] show that a didjeridu player typically uses a pressure of about 1-2 kPa (10-20 cm water gauge
pressure) for the drone note and about 4-5 kPa to produce the second mode. Some players can produce the third mode and even higher modes, but
they are rarely used. Indeed, even the second mode is only employed for brief accents, and not as a sustained tone.
4. SOUND QUALITY
The discussion above is essentially linear and expressed in terms of linear quantities such as acoustic admittances. Sound production
in wind instruments, however, is a non-linear process [5,11], and this non-linearity is responsible for generating the upper partials of the tone.
The process has been examined for brass instruments such as the trumpet [12] and trombone [13] and much of this discussion can be applied to the didjeridu.
Because, unlike the reed valve in a clarinet, the lip valve operates at very nearly its resonance frequency [7,9,10], the motion of the player's lips is nearly sinusoidal. The average lip opening is determined
by the blowing pressure, and the amplitude of the lip vibration is such that the lips just about close once in each cycle. If P0 is
the steady blowing pressure, p the pressure just inside the mouthpiece of the instrument, and x = a0 + a sin 2pi ft the
lip opening, then the volume flow U through the lip valve is
where y is a constant. The pressure p inside the instrument mouthpiece is approximately RU, where R is
the acoustic resistance of the instrument tube at the resonance frequency f1, and we can substitute this back into (3), along
with the expression for x, to find, after a little algebra, that if a < a0 the flow has the form
This expression cannot be taken too literally in the limit as a ® a0, but the shape of the flow waveform is essentially
as shown in Fig. 3.
Clearly such a waveform has many harmonics, and this accounts for the rich sound of the didjeridu, and of lip-excited instruments
in general. The relative strengths of the upper harmonics are not well predicted by this simple flow waveform, however, for several reasons.
The flow waveform gives a spectral envelope which is initially nearly constant and then declines at about 12 dB/octave. The assumption that R is
constant, however, is not very good, and this resistance is less for the upper harmonics than for the resonant fundamental, except for accidental
near-coincidences with higher horn resonances. Finally, the transfer function between flow spectrum and acoustic radiation rises at 6 dB/octave
at low frequencies and is then flat above about 3 kHz for the didjeridu horn. Despite these reservations, however, this simple treatment does
give a fair idea of spectral behaviour.
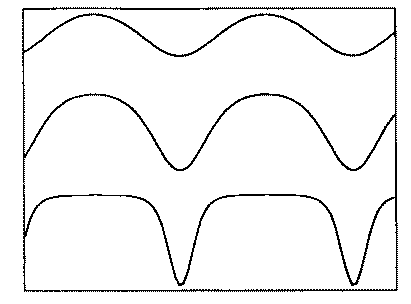
Figure 3. The flow waveform through a lip-valve at several amplitude levels, as given by Equation (4).
Note that the sound spectrum of the didjeridu, as for all sustained-tone instruments (except when playing "multiphonics" or
other special effects), is strictly harmonic. The fact that the upper modes of the pipe are not in harmonic relation to the fundamental affects
only the strength of certain harmonics. If one of the upper pipe modes is sounded instead of the fundamental, then this sound will itself be
accompanied by its own set of harmonics.
We should now consider the effect of the player's mouth cavity on sound quality. The player's lip opening varies nearly sinusoidally
with time, as we have seen. The time spent at each opening is inversely proportional to the lip speed at that opening. If the lips just close
each cycle so that a = a0, the fraction of time spent at opening x can then be shown to be proportional to [x(2a0 - x)]-1 which
is sharply peaked at x = 0 and 2a0, so that the lips spend most of their time either nearly fully open or nearly closed.
Seen from the instrument tube, therefore, the player's mouth is mostly either blocked off by the closed lips or else forms a Helmholtz resonator
consisting of a closed volume vented by the lip opening. The resonance frequency of this resonator can be estimated from our experience with
whistling, in which the whistle frequency is the resonance frequency of the same Helmholtz resonator. Since the lip opening is similar, within
a factor of less than ten, in the two cases, the attainable resonance frequencies should be the same within about a factor three. We therefore
expect that it should be possible to vary the resonator frequency over a range from about 500 Hz to about 3 kHz by changing the mouth volume
with the tongue.
It is fairly easy to understand the effect of such a resonator on the lip-valve flow and hence on the radiated sound spectrum.
The resonator is rather highly damped by the flow resistance through the lip valve so that its bandwidth encompasses the frequencies of several
harmonics of the drone frequency. The acoustic flow through the lip valve will be enhanced for these harmonics, so that the acoustic spectrum
will exhibit a "formant band" rather like those of the human voice and, indeed, arising from similar causes. Details are more complicated than
this, of course, because the opening from the mouth to the instrument is changing with time. While the didjeridu can be played with a dull drone,
lacking obvious formants, this is not usual for good players. Fig. 4 shows two examples of such formants, which play an important role in producing
the characteristic sound of the didjeridu. In the first example, there is a pronounced formant band at about 1500 Hz, while in the second example
the player has reduced the volume of his mouth so as to raise formant frequency to about 2.2 kHz. In each case there is some evidence for a lower
vocal-tract formant at about 500 Hz. Because the frequency range of these formants is similar to that of human vowel formants, they have a similar
aural effect. In normal playing, using circular breathing, these formants are produced in a rhythmic manner as the mouth volume changes, but
they are often made a tonal feature of the performance.
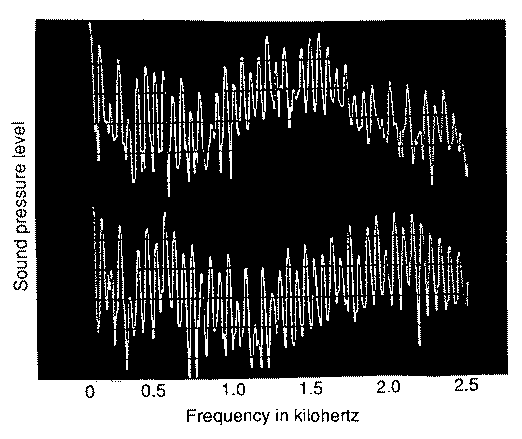
Figure 4. Formant bands in the didjeridu sound. In the upper trace, there is a mouth-cavity formant at about 1.5 kHz,
while in the lower trace this has been shifted to about 2.2 kHz by constricting the mouth.
These formant phenomena are much more pronounced in the didjeridu than in Western brass instruments, principally because trumpets,
tubas and the like have a cup-shaped mouthpiece with a narrow constriction between it and the main bore of the instrument. This mouthpiece, as
well as providing a comfortable support for the lips, functions as a Helmholtz resonator in its own right, and its resonance produces a broad
formant band, typically with a centre frequency around 500 Hz for a trumpet [5]. The mouthpiece cavity also functions as a filter which reduces any influence that mouth
resonances might have on upper partials of the sound.
There is one other aspect of performance technique that deserves detailed acoustic comment. This is the use of vocal sounds
to augment the drone of the didjeridu. Because of the acoustic coupling between the vocal folds in the throat and the player's vibrating lips,
the interaction is quite complex. Suppose that the player's vocal folds vibrate at a frequency fV. Then this produces pulses
of flow in the same way as described for the lip valve and illustrated in Fig. 3. The flow entering the mouth, and therefore the mouth pressure p0 of
(4), thus contains all harmonics nfV of the vocal-fold frequency. When this flow is convolved with the nonlinear flow through
the lips, which are vibrating with frequency fL, as in (4), the result is the production of all frequencies nfV ± mfL,
those with greatest amplitude having small integer values (l or 2) for m and n.
The simplest example of this frequency mixing occurs when the player sings a steady tone at a frequency simply related to the
drone frequency. A typical example is the singing of a note that is a just major tenth (frequency ratio 5/2) above the drone fundamental. The
cross term fV - 2fL then has a frequency fL/2 and this is accompanied by all its harmonics from
the other cross terms. The sound is therefore an octave below the original drone frequency. There is not be much radiated energy in this sub-octave
fundamental, but the subjective pitch is generated strongly from the sequence of harmonics. Because of the low pitch and the strength of the
higher harmonics, the sound has a rough rasping quality which is very effective. A rather similar result can be obtained by singing a note a
perfect fifth (frequency ratio 3/2) above the drone fundamental.
Finally, we should remark that players of the instrument often use it to accompany traditional songs or stories and, to this
end, embellish their playing by adding the sung sounds of barking dingoes, brolgas and other animals. The pitch of these vocal sounds is rather
high so that frequency mixing does not have such a pronounced effect, and the sounds can be made easily recognisable.
Fig. 5 shows a spectral display of a short passage of didjeridu playing. In this representation, time is along the horizontal
axis and frequency on the vertical axis, with the density of shading indicating the sound pressure level. Two things are immediately obvious.
The first is that the harmonic structure of the sound is clearly evident in the closely spaced dark bands running horizontally in the figure.
The second feature is the formant bands, which show up as darker regions on the plot and vary with time. Articulation and circular breathing
divide the time record into repeating segments. Features of this type will be familiar to anyone involved with human speech analysis.
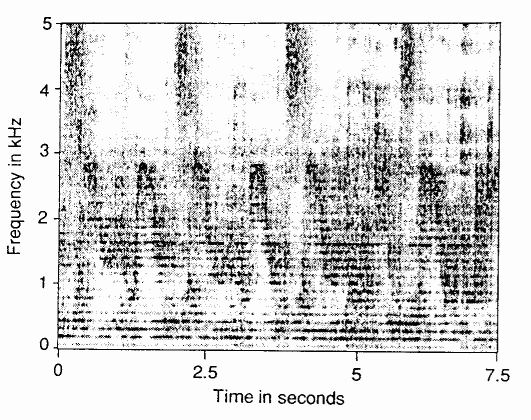
Figure 5. Time-frequency display of the sound of a didjeridu during a typical playing sequence.
Note the harmonics of the drone frequency, the shifting formant bands, and the articulation noise.
5.CONCLUSION
Although the didjeridu is physically a simple instrument and its makers appear to accept wide variations in its physical dimensions
and therefore in its tuning, it supports a wide variety of subtle performance techniques. We have considered here the acoustics of only the most
important of these, but it is clear that there is a great deal of interesting understanding to be derived. I hope that this paper may serve as
an example of the sort of results that can come from cooperation between acousticians and musicologists.
Acknowledgments
The work on which this paper is based was completed a long time ago and has, for the most part, already been published elsewhere [1]. It is a pleasure to acknowledge the help I have received from conversations with Trevor
Jones, a distinguished musicologist and expert didjeridu player, and with Graham Wiggins, a physicist turned didjeridu virtuoso. Some of the
analysed examples were played by Trevor and some were collected in the field by linguist Bill Hoddinott. I would also like to thank Suszanne
Thwaites for assistance with the measurements.
References
- N.H. Fletcher, "Acoustics of the Australian didjeridu", Australian Aboriginal Studies No.1, 28-37 (1983)
- G.C. Wiggins, "The physics of the didgeridoo", Physics Bulletin 39, 266-267 (1988)
- T.A. Jones, "The didjeridu", Studies in Music University of Western Australia 1, 23-55 (1967)
- T.A. Jones, "The yiraki (didjeridu) in North-eastern Arnhem Land: Techniques and styles", in The Australian Aboriginal Heritage ed.
R.M. Berndt and E.S. Phillips, Australian Society for Education through the Arts, in association with Ure Smith, Sydney (1973) pp. 269-274
- N.H. Fletcher and T.D. Rossing, The Physics of Musical Instruments Springer-Verlag, New York (1991) pp. 191-193, 369-372, 378-388
- H. Helmholtz, On the Sensations of Tone (1885) trans. A.J. Ellis, Dover, New York (1954)
- S. Yoshikawa, "Acoustical behaviour of brass player's lips", J. Acoust. Soc. Am. 97, 1929-1939 (1995)
- K. Ishizaka and J.L. Flanagan, "Synthesis of voiced sounds from a two-mass model of the vocal cords", Bell Syst. Tech. J. 51,
1233-1268 (1972)
- N.H. Fletcher, "Excitation mechanisms in woodwind and brass instruments", Acustica 43, 63-72 (1979)
- N.H. Fletcher, "Autonomous vibration of simple pressure-controlled valves in gas flows", J. Acoust. Soc. Am. 93, 2172-2180
(1993)
- N.H. Fletcher, "Nonlinear theory of musical wind instruments" Applied Acoustics 30, 85-115 (1990)
- J. Backus and T.C. Hundley, "Harmonic generation in the trumpet", J. Acoust. Soc. Am. 49,509-519 (1971)
- S.J. Elliott and J.M. Bowsher, "Regeneration in brass wind instruments", J. Sound and Vib. 83, 181-217 (1982)
Source for this article: Acoustics Australia, Vol 24, pp 11-15 (1996)
Reprinted with permission of the author Neville Fletcher
For more interesting information on physics and musical instrument accoustics check out www.phys.unsw.edu.au
Read on:
Physics of the Didgeridoo
Physics of the Didgeridoo - End Correction
In Depth Physics of the Didgeridoo
Australian Aboriginal Musical Instruments - The Didjeridu, The Bullroarer And The Gumleaf
The Physics of Dreamtime: An analysis of the acoustical properties of a didgeridoo
Vocal Tract Resonances and the Sound of the Australian Didjeridu (Yidaki)
What Makes a Good Didj? |