#110106485
Benjamin Hammond
PHYS 225 Musical Acoustic
Professor dik Harris
As a musician, the didgeridoo has fascinated me since my trip to Australia as a child. Through a friend, we were able to visit
an Aborigine reservation, and they showed my brother and I the basics of playing it (of course the girls were not allowed, but my sister was
taught to carry baskets of food on her head). Though at the time I was capable of little more than a glorified burp, my father purchased one,
and more importantly some recordings featuring expert didgeridoo players. Over time I developed the circular breathing technique needed to play
the didge, and tried to mimic the sounds I heard on the recordings. Then, with the growing popularity of repetitive, rhythmic, electronically-based
music, the didgeridoo began appearing in popular music, no longer being simply a cultural oddity. For these reasons and more, I have decided
to take a closer look at the didgeridoo not from a musician's perspective, but from that of a physicist. I would like to explore what it is about
both the way the didge is played and constructed that gives it such a unique, characteristic sound. Specifically, what are the respective roles
of: the pipe itself, the player's vocal tract, the playing technique, and the interaction of vocalizations with the didgeridoo tone.
To a musicologist, the didgeridoo, (also didjeridu or yiraki) represents a glimpse of perhaps the most ancient music. Traditionally
played by a select few tribes in Northern Australia, the didgeridoo is quite possibly one of the first musical instruments. To the inventive
musician or composer, the didgeridoo offers a rich texture of sound, which sets it apart from many other instruments. To the physicist however,
the didgeridoo is most simply a hollow pipe. Normally somewhere between 100 to 200 cm long and 8 to 10 cm in diameter, the didgeridoo requires
little else beyond a branch, termites and patience to create. After finding a termite-infested branch, an instrument maker will drop a burning
coal inside and create a relatively smoothed out hollow tube. As final finishing steps, tribal paintings are applied to the outside, and sometimes
a beeswax mouthpiece is added to one opening. (Fletcher, 1)
Due to the inherent irregularities and inconsistencies of almost every step of the construction, each didge is completely unique.
Not only does the timbre of the instrument differ, but also the fundamental pitch of the instrument will differ even by a difference of an octave
between instruments (lengths being anywhere from 1 to 2 meters). However, at its most basic level, it is a relatively close model to simply refer
to the didge as an open-closed pipe. The formula for determining the fundamental frequency of an open-closed pipe (based on the reflections of
air pressure) is given as F = v /4L where F is the fundamental frequency, v is the speed of sound, and L is the length of the tube, or
in this case the didgeridoo (Rossing, 65). It's interesting to note that the length of a trumpet unfurled (140 cm) is actually about the
same length as many didgeridoos (between 100 and 200 cm). The reason the didge seems like a lower instrument is that… it plays lower!
Trumpets and most other brass players rarely if ever utilize the lowest mode of vibration, also known as the fundamental and the pedal tone.
In looking at information presented by Rossing, it's shown that this mode is musically useless as compared to the others, because none of the
natural resonances of the instrument (with the carefully constructed bell, valves and mouth piece) line up with this frequency. The input impedance
is not string enough to produce a great sound. Therefore the sound is not clear, and it's much harder for the player to set up an oscillation
(Rossing, 232). In reality, it's not that this mode is that bad, it's just that it's not as good as the rest. In a didgeridoo on the other
hand, because of the lack of a mouthpiece and a bell, this mode turns out to be more useful than the others. In normal playing, this is basically
the only mode that is used, except the second for brief accents or animal noises. In this respect, the aforementioned formula F = v /4L is
even more fitting, because it calculates the lowest mode. 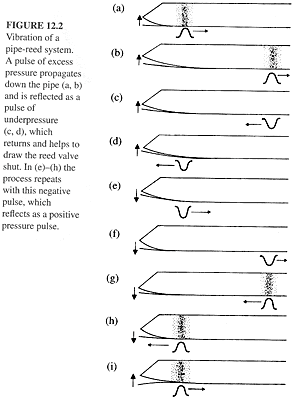 Given
the properties of air reflections, this formula is easy to explain. A positive pulse at the closed end (your mouth) will travel the length of
the tube, reflect as a negative pulse when it reaches the open end, reflect against your lips (now closed) as a negative, then travel down the
tube again still as a negative, hit the open end a second time reflecting as a positive, and finally returning to your lips as a positive, completing
the cycle for a total of 4 trips the length of the pipe. See diagram. Using this formula it is easy to calculate roughly what the fundamental
should be for a tube (Rossing, 65). Given
the properties of air reflections, this formula is easy to explain. A positive pulse at the closed end (your mouth) will travel the length of
the tube, reflect as a negative pulse when it reaches the open end, reflect against your lips (now closed) as a negative, then travel down the
tube again still as a negative, hit the open end a second time reflecting as a positive, and finally returning to your lips as a positive, completing
the cycle for a total of 4 trips the length of the pipe. See diagram. Using this formula it is easy to calculate roughly what the fundamental
should be for a tube (Rossing, 65).
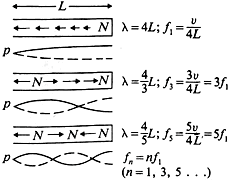 This formula can again
be used (with some alterations) to determine the frequencies of the modes of vibration beyond just the fundamental. The extra alteration needed
is the fact that open-closed pipes only have modes at the odd numbered harmonics. This occurs because of the opposite reflecting properties of
the open and closed ends, meaning there are half the numbers of waveforms that can fit inside of a pipe (as compared to an open-open pipe). See
diagram. Suffice it to say that in this simple model, a didgeridoo is an open-closed pipe, which has resonate modes at v/4L, 3v/4L, 5v/4L etc
(though again only the first is regularly used) (Rossing, 65). It is important to note however, the assumptions and simplifications made
to arrive at this formula. First of all, a didgeridoo is anything but uniform, and is certainly not a "perfect" pipe in a physics sense.
Normally there is a slight flare at one end, which has not been taken into account at this point, and moreover the material of the didgeridoo
has been completely disregarded. While both of these simplifications will skew our estimations, they are "close enough" for this basic
analysis. Later on I will show how close the measurements I've done on my own didgeridoo are to the "perfect" calculated measurements. This formula can again
be used (with some alterations) to determine the frequencies of the modes of vibration beyond just the fundamental. The extra alteration needed
is the fact that open-closed pipes only have modes at the odd numbered harmonics. This occurs because of the opposite reflecting properties of
the open and closed ends, meaning there are half the numbers of waveforms that can fit inside of a pipe (as compared to an open-open pipe). See
diagram. Suffice it to say that in this simple model, a didgeridoo is an open-closed pipe, which has resonate modes at v/4L, 3v/4L, 5v/4L etc
(though again only the first is regularly used) (Rossing, 65). It is important to note however, the assumptions and simplifications made
to arrive at this formula. First of all, a didgeridoo is anything but uniform, and is certainly not a "perfect" pipe in a physics sense.
Normally there is a slight flare at one end, which has not been taken into account at this point, and moreover the material of the didgeridoo
has been completely disregarded. While both of these simplifications will skew our estimations, they are "close enough" for this basic
analysis. Later on I will show how close the measurements I've done on my own didgeridoo are to the "perfect" calculated measurements.
These simplifications are of minor importance, but more relevant to the point of the paper, the analysis of that unique "didge" sound,
is the driving mechanism, or the mouth. Many instruments are played using wind pressure and or vibrational pulses from the mouth, but the didgeridoo
in particular requires a strong diaphragm and a dexterous mouth. A very basic simplification of the mouth in this regard is the same for both
reeds and brass instruments, and is commonly referred to as a pressure controlled valve. In this system, wind pressure (in this case from the
diaphragm) is alternately blocked and released by a moving element, in this case your lips (see first diagram).
These intermittent pulses of air cause the air inside the instrument to vibrate at a certain frequency, as described in the
above section. To obtain these frequencies, air must be added at the correct interval; otherwise the system will not oscillate. According to
Rossing, "It would be difficult, if not impossible, for the player to synchronize his or her lips opening by muscular action alone; fortunately
this is not necessary. Pressure pulses reflected back from the horn tend to force the player's lips open at the right time during the cycle of
oscillation" (Rossing, 228-9). This positive feedback allows the player to produce the proper timing needed to resonate the pipe
at the correct times and line up with the natural modes cause by the input impedance.
So, after all of this, we have still accounted only for the basic "drone" fundamental, which is certainly not unique,
and is probably the least interesting element of the didge's sound. Much more interesting is to look in detail at the interaction of the vocal
tract and the higher harmonics of this fundamental. It is important to note that while the didgeridoo's modes are not in integer relation (because
the varying width of the pipe), the harmonics of any given mode are (Didgeridoo and Vocal Tract, 1). These harmonics are far more important
anyways, considering the infrequent use of the other modes. Given this piece of information, we still have not accounted for the vast difference
in timbre between the didge and a more traditional brass instrument. These differences are attributed to much more complex elements, which in
fact are still being researched by the authors found on my works cited page. For example, the latest research I have found (done in 2001) includes
MRI scans of the player's vocal tract while playing, to scientifically understand what is occurring within the player himself. In actuality,
the fact that the player's mouth is so involved in the sound production is what gives the didge its complex sound.
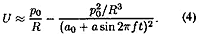 In a traditional brass
instrument, as in a didge, air-pressure responds nonlinearly, and this is what gives these instruments their rich character. In Fletcher's article,
he gives a quite complicated expression to represent the vibration of a player's lips within a given horn. Though the math behind the
formula is complex and a bit confusing, In a traditional brass
instrument, as in a didge, air-pressure responds nonlinearly, and this is what gives these instruments their rich character. In Fletcher's article,
he gives a quite complicated expression to represent the vibration of a player's lips within a given horn. Though the math behind the
formula is complex and a bit confusing,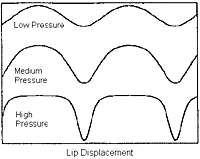 the
graph associated with the formula exhibits quite clearly why more air in the didge gives more harmonics. The nearly pure sine wave present
at low pressure would correspond to the Fourier analysis of any "dull" sound, with few harmonic components. Then, as the pressure is
increased, the graph response becomes sharper, giving the "brighter" sound associated with a square wave or other harmonically rich,
straight waveforms. This is one part of what causes the didge's timbral modulation. (Fletcher, 1) the
graph associated with the formula exhibits quite clearly why more air in the didge gives more harmonics. The nearly pure sine wave present
at low pressure would correspond to the Fourier analysis of any "dull" sound, with few harmonic components. Then, as the pressure is
increased, the graph response becomes sharper, giving the "brighter" sound associated with a square wave or other harmonically rich,
straight waveforms. This is one part of what causes the didge's timbral modulation. (Fletcher, 1)
The other timbral aspect, in this case distinct from other brass type instruments, is the aforementioned role of the player's
oral cavity in the oscillation. In other brass elements, the mouthpiece serves to regulate the airflow into the horn. Additionally, the mouthpiece
itself resonates and adds a formant frequency to the sound. Holding the separate mouthpiece and slapping an open palm down onto the top one can
find this "popping" frequency. In the article Physics of the Didjeridu, Fletcher states that "this
mouthpiece, … functions as a Helmholtz resonator in its own right, and its resonance produces a broad formant band…The mouthpiece
cavity also functions as a filter which reduces any influence that mouth resonances might have on upper partials of the sound." This is
the complete opposite of the didgeridoo, in which the only "mouthpiece" is a rim of beeswax to provide a better seal. Since the mouth
is literally inside the instrument, the shape of the jaw and the position of the tongue adds at least one resonant chamber, or a formant band,
similar to that of a singer. As the advanced didgeridoo player changes the shape of his mouth, the harmonic content is modulated accordingly.
The addition of a mouthpiece on a tube (i.e. trumpet) adds one formant from the mouthpiece itself, but also minimizes the presence of the other
resonances produced by the mouth cavity, the throat, and the larynx.
In fact, this lack of a mouthpiece is not the only "flaw" exploited in the playing of the didge. Perhaps the most
characteristic elements of the didge's sound are due to the circular breathing which is required to play the instrument for any length of time.
The Acoustical Impedance (Za) is a measure of the needed pressure per volume, given by Za = 400 / S (where in this case S is the cross
sectional area of the tube in m2) (Rossing, 67). It's important to note that the Acoustical Impedance and the area are inversely
related, and that every change in diameter will result in a reflection of some sound waves. This inverse relationship also explains why the didge
takes so much more air than the trumpet. The radius of a trumpet tube to be approximately a third of a didge tube, so in my didge the acoustical
impedance is 400 / (3.14*32) = 14.2 and in a standard trumpet, it would be 400 / 3.14*0.62) = 326.8 (Rossing,
227). This lower impedance value means the player is forced to use remarkably more air, somewhere around 2 kPa (Fletcher, 1). As human
lungs can only hold so much air, players must "circularly breath" to produce a musical tone long enough to vary the sound appropriately.
To do so, one must use their cheeks as bellows, and alternate between normal blowing (using the diaphragm), and a simultaneous combination of
constricting the cheeks, pushing out the tongue, and breathing in through the nose. A complicated process surely, but one which occurs in other
cultures, and has even been adopted by players of Western wind instruments in recent years. Though the intention is a consistent stream of air,
the resultant sound is anything but consistent. By constantly repositioning the mouth to complete the breathing process, all of the associated
timbral changes take place, altering the sound of the instrument. Instead of being a hindrance, the skilled didgeridoo player will capitalize
on this effect, and use the rhythms caused by this modulation to give a tempo and movement to the song. In this respect, the didge is second
perhaps only to the voice in its connection to the player. Its impossible for the player to not to be entirely engaged in the music, as the rhythm
of the instrument is tied directly to the rhythm of the body.
In theory, all of these models and calculations make sense, but how close to reality are they, especially given the numerous
assumptions and approximation I have made? To explore this question, I will compare the spectral plot of my didge, playing different "tones" (accentuating
different harmonics by changing the shape of my mouth), and see how closely the resulting sound spectrum is to the theoretical model. The first
most basic step is to determine the fundamental of my didgeridoo and compare it to a theoretical straight tube of the same length. Mine is 63
inches long, or about 1.60 meters. Using the open closed formula from above, F = v /4L I get a fundamental of 53.75 Hz. This is
lower than the actual pitch of the pipe, at about 63 Hz. Though not exactly the same number as given from the simplest model of a pipe,
this seems to work when taking into account the adjustment for the flared end, which raises the lowest mode of vibration. So the most basic element
was close, how about the rest of the harmonics? For this I have recorded myself playing four different ways, accenting different harmonics making
a high, medium high, medium low, and low. Certainly there are far better didgeridoo players than myself, but for my purposes a single sustained
tone was preferable to the sweeping changes and vocalizations that characterize professional playing. Taking FFT plots of these recordings, I
can examine the specific waveforms present in each example, and compare to the theory described above. Remarkably, and reassuringly, the graphs
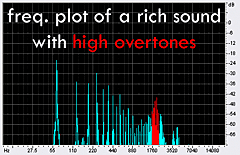
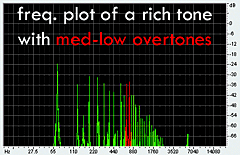
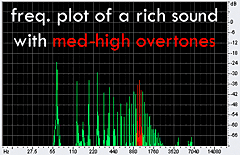
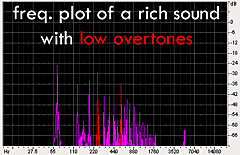
produced from the sound of my actual didge correspond quite well to the projected data. It's easy to see that when I raised my tongue and jaw
into the highest position, a whole crop of overtones appeared in the 1800 Hz region. The other plots produce the same results: as I lower my
tongue and jaw in different increments, the overtones (in red) shift respectively from 1800 Hz, 1100 Hz, 760 Hz and 560 Hz. This corresponds
exactly with the theoretical model that a constricted vocal tract accentuates the higher overtones. |
These graphs provide some other interesting spectral information, which can be compared with the hypothetical model to assess
accuracy. According to theory, in an open-closed cylindrical pipe the radiation efficiency will increase as f2 up to a certain cutoff frequency
which is determined by f = c / pi*a where "c" is speed of sound in the pipe and "a" is the radius of that pipe (Rossing,
237). In "normal" brass instruments such as a trumpet and trombone, the cutoff frequency will be significantly lower, due to the
presence of a bell. Since the didgeridoo has only a slight flare in the end, (and mine less than most), and there is no bell to lower that cutoff,
the frequency for my instrument (4.5 cm radius at the "bell end") should be f = 344 / (3.14*0.045) = 2434 Hz. By looking at the
graph, it's easy to see that the majority of the sound does in fact die away near this region, in each of the plots above. There is noise above
this dip, but it is important to note that my calculations were done with less then scientifically precise equipment, and that ambient noise gives
rise to a lot of hiss and other high frequency range noise that is not actually produced by the instrument. Just to reaffirm my predictions about
the noise floor, I did an FFT plot of "silence" in between didge playing, and the resultant noise was a band in all frequencies up to
about -80 dB, with a slight presence around 4000 Hz. Taking into account this noise floor, (and adjusting the graphs so the lowest plotted value
was -72 dB) I would say the calculations were quite accurate for this instrument, especially given the "spherical cow" of my didge being
a straight pipe with no flare and no absorption of sound. Both of these assumptions are outright wrong, but nicely enough they don't throw off
the calculation by much (or at least they counteract each other  ). ).
Looking at these graphs, it's easy to see that the fundamental appears at around 63 Hz, and then the overtones appear in decreasing
intensity (for the most part) consistent with the input impedance of a pipe, until the various accentuated regions, and then they quickly die
away after hitting the cutoff frequency. I say that the overtones appear in decreasing intensity "for the most part" because in addition
to the intentional accentuation, there is a spike at around 300 Hz is which is significantly louder than its neighbors in all the tones, and
is the loudest component besides the drone fundamental. The spike at around 170 Hz also seems to be a bit louder than one would expect from the
curve of the rest of the amplitudes and the original input impedance of a pipe. Due to the limited research previously done on didgeridoos coupled
with the completely unique characteristics of every didgeridoo, I have nothing but an educated guess as to why these frequency components appear
where they do.
One way to figure out where sounds are coming from is to plug in the frequency we know we are getting, and seeing what length
tubing or what size mechanism we need to produce this pitch. In the case of the accentuated overtones, using the formula for and open closed
pipe f = c / 4 L, I get lengths of around 5 cm, 8 cm, 11 cm, and 15 cm for the frequencies highlighted in red on the graphs. I
have not measured the inside of my mouth, and surely the irregular shape would affect the numbers, but these lengths seem reasonable to match
up with the length from the opening of my mouth to the close made by my tongue, depending on the position of my jaw. Using another method which
is slightly less scientific, but a bit more common sensible, I played an overtone, then simply removed the didge and pushed air through without
changing the shape of my mouth. Expectedly, this "whistling" tone was the exact same pitch as the overtone I had made with the didge
in place, implying that the resonance was due to the shape of my mouth.
As for the second, lower structure I am even less sure of my answer, but my guess would be that it is caused by the shape of
the instrument and not by my mouth. Firstly, it did not vary in intensity in different mouth positions, implying that it was not directly tied
to the shape of my body. Secondly, using the same formula as above, the length of "tubing" needed would be 344 / 300 / 4 = 30 cm.
For the other slightly raised frequency at about 170 Hz, the distance would be 344 / 170 / 4 = 50 cm. In looking at the shape of my didgeridoo,
it's quite apparent that it is anything but straight. There are actually two fairly significant bends where the tube changes in diameter and
the pipe veers off to one side. The first of these crooks appears about 34 cm from the beeswax mouthpiece, and the second appears at about 49
cm from the slightly flared end. Since changes in diameter give a change in Acoustic Impedance, and therefore a place for reflection (an
opening being an infinite change in diameter), it's reasonable to assume that these irregularities in the shape of the didgeridoo are strengthening
the overtones its fundamental. The fundamental is at around 63 Hz, and produces integer harmonics thereafter. When one of these harmonics lines
up near a resonance of the pipe, that overtone is strengthened, thus causing the distinct sound of each instrument.
The last characteristic of the didge is one of the most interesting audibly, and also probably the most unique to the didgeridoo.
In most didgeridoo music, the sound is used to accompany story telling or ceremonies, and therefore regularly mimics the noises of nature, such
as bush animals and thunder. By both singing and making other vocalizations while simultaneously playing the didgeridoo, the player can produce
an amazing array of sounds, ranging from realistic to outright scary. Depending on the desired effect, the player will use the voice to control
the sound of the didge, or vice-versa. What is most interesting however, is the strong presence of difference tones while using this technique. "Discovered" by
Italian violinist Tartini in 1714, the difference tone is a synthetic tone that occurs when two pitches are played simultaneously. The pitch
of this resultant tone is actually the difference between the first two, fdiff = (f1 - f2), and is accurately called the quadratic
difference tone (Rossing, 157-160). There are other combination tones possible, most noticeably the cubic difference tones fcubic_diff =
(2*f1 - f2) and fcubic_diff = (f1 - 2*f2). Normally these tones are most noticeable between two loud high-pitched instruments,
such as tin whistles or shrill sopranos. They can however be produced by any two pitches, and will be heard as long as the amplitudes and ranges
are suitable. These tones occur quite often in didgeridoo playing, but are usually perceived as extremely low rumblings or added depth of the
original sound rather than distinct tones.
To demonstrate, I have recording myself playing the fundamental (63 Hz) and singing a Major Tenth above it (159 Hz). It's easy
to see on this plot (as compared with the non-vocalization plots shown earlier) that there are numerous additional frequency components.
Note that the Major Tenth spike (shown in blue at 159 Hz) is much larger than in the other graphs.
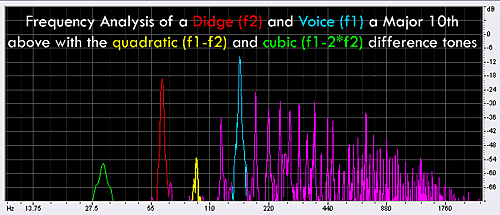
It's very small in the other graphs because a perfect cylinder blown on one end will only produce the odd harmonics. However,
the didge is not even close to perfect, and the third does reflect and oscillate at least a bit. In this case however, I am singing the pitch,
so it's much stronger, and it has all of the overtones that my voice produces as well. By doing the math, we can derive the quadratic difference
tone (159-63) = 93 Hz (shown in yellow) and also one of the cubic difference tones (159 - 2*63) = 33 Hz (shown in green). These
tones are both quite large spikes that are not present at all on the non-vocalization plots above. Though they are difficult to hear on a recording,
in live performance (perhaps assisted by the resonance mode of my room?) the lowest sub-fundamental pitch was very apparent. It is also quite
possible that given the right conditions, lower, even subsonic tones can be created, and in this aspect produce an even larger range of sounds
and textures.
Ultimately with this instrument, it is important to keep the context, and consider the entire experience of a didgeridoo performance.
Accompanied by dramatic story telling, ritualistic dancing, singing or other didgeridoos, the instrument works much more effectively in a live
context than on graphs or recordings. Though this is true of every instrument, it is probably most important for the didgeridoo. The extreme
range both musically, from 20 Hz to 2500 Hz, and emotionally provide this instrument with mimicking and dramatic capabilities unrivaled by most
other instruments, Western or otherwise.
In this paper I have examined, to the best of my abilities, the various contributions of; the didgeridoo as a open-closed pipe
model, the vocal tract as an extension and resonating chamber for the didgeridoo, the effect of circular breathing on the harmonic content, and
some of the acoustical oddities that arise when combining a sung tone with a blown tone. However, what is important, and in my opinion ultimately
more interesting, is to look at these simple physical models and calculations, and use them to determine why the human ears (and brain) are drawn
to this unique sound. What is it about the dynamic range, the rhythmic drone or the associated rituals that keeps this indefinitely aged instrument
so popular in the music scene, from local drum circles and jam sessions to World Music and Techno CD's worldwide. There is still much research
to be done on the didgeridoo, as there have been but few researchers interested, but what has been discovered continues to motivate those few
people to dig even deeper into the mysteries of this deceptively simple instrument.
Works Cited
- Rossing, Moore and Wheeler. The Science of Sound. 3rd Ed.
- Fletcher, Neville. "The Physics of the Didgeridoo:" https://www.didjshop.com/physicsDidj03.html Research
School of Physical Sciences. Australian National University
- Fletcher, N., Hollenberg, L., Smith, J. and Wolfe, J. (2001) "The didjeridu and the vocal tract" Proc. International Symposium
on Musical Acoustics, Perugia. D.Bonsi, D.Gonzalez, D.Stanzial, eds, pp 87-90. (.pdf file) http://www.phys.unsw.edu.au/~jw/ISMAdidjpaper.pdf
All FFT Plots were done using my didgeridoo and CoolEditPro.
All other charts were from Rossing's book.
Audio Samples
Didge with a "dull tone"
Didge with a "rich tone"
Modulating the harmonic content by changing shape/position of mouth
Circular breathing, affecting harmonic content
Example of Didge drone with Vocalizations
Didge drone with a sung tone a Twelth (Fifth + Octave) above
Didge drone with a sung tone a Major Twelth (Third + Octave) above
Copyright: Benjamin Hammond, http://www.benjaminhammond.com/didge/
The above text and audio files were published on this web site with the author's permission.
Disclaimer: The Didjshop is not responsible for the accuracy of the above material and the opinions expressed in the above
text are the views and opinions of the author.
Read on:
Physics of the Didgeridoo
Physics of the Didgeridoo - End Correction
In Depth Physics of the Didgeridoo
Australian Aboriginal Musical Instruments - The Didjeridu, The Bullroarer And The Gumleaf
Vocal Tract Resonances and the Sound of the Australian Didjeridu (Yidaki)
What Makes a Good Didj? |

 Given
the properties of air reflections, this formula is easy to explain. A positive pulse at the closed end (your mouth) will travel the length of
the tube, reflect as a negative pulse when it reaches the open end, reflect against your lips (now closed) as a negative, then travel down the
tube again still as a negative, hit the open end a second time reflecting as a positive, and finally returning to your lips as a positive, completing
the cycle for a total of 4 trips the length of the pipe. See diagram. Using this formula it is easy to calculate roughly what the fundamental
should be for a tube (Rossing, 65).
Given
the properties of air reflections, this formula is easy to explain. A positive pulse at the closed end (your mouth) will travel the length of
the tube, reflect as a negative pulse when it reaches the open end, reflect against your lips (now closed) as a negative, then travel down the
tube again still as a negative, hit the open end a second time reflecting as a positive, and finally returning to your lips as a positive, completing
the cycle for a total of 4 trips the length of the pipe. See diagram. Using this formula it is easy to calculate roughly what the fundamental
should be for a tube (Rossing, 65).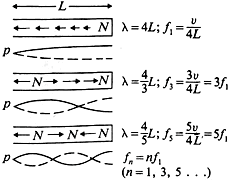 This formula can again
be used (with some alterations) to determine the frequencies of the modes of vibration beyond just the fundamental. The extra alteration needed
is the fact that open-closed pipes only have modes at the odd numbered harmonics. This occurs because of the opposite reflecting properties of
the open and closed ends, meaning there are half the numbers of waveforms that can fit inside of a pipe (as compared to an open-open pipe). See
diagram. Suffice it to say that in this simple model, a didgeridoo is an open-closed pipe, which has resonate modes at v/4L, 3v/4L, 5v/4L etc
(though again only the first is regularly used) (Rossing, 65). It is important to note however, the assumptions and simplifications made
to arrive at this formula. First of all, a didgeridoo is anything but uniform, and is certainly not a "perfect" pipe in a physics sense.
Normally there is a slight flare at one end, which has not been taken into account at this point, and moreover the material of the didgeridoo
has been completely disregarded. While both of these simplifications will skew our estimations, they are "close enough" for this basic
analysis. Later on I will show how close the measurements I've done on my own didgeridoo are to the "perfect" calculated measurements.
This formula can again
be used (with some alterations) to determine the frequencies of the modes of vibration beyond just the fundamental. The extra alteration needed
is the fact that open-closed pipes only have modes at the odd numbered harmonics. This occurs because of the opposite reflecting properties of
the open and closed ends, meaning there are half the numbers of waveforms that can fit inside of a pipe (as compared to an open-open pipe). See
diagram. Suffice it to say that in this simple model, a didgeridoo is an open-closed pipe, which has resonate modes at v/4L, 3v/4L, 5v/4L etc
(though again only the first is regularly used) (Rossing, 65). It is important to note however, the assumptions and simplifications made
to arrive at this formula. First of all, a didgeridoo is anything but uniform, and is certainly not a "perfect" pipe in a physics sense.
Normally there is a slight flare at one end, which has not been taken into account at this point, and moreover the material of the didgeridoo
has been completely disregarded. While both of these simplifications will skew our estimations, they are "close enough" for this basic
analysis. Later on I will show how close the measurements I've done on my own didgeridoo are to the "perfect" calculated measurements. the
graph associated with the formula exhibits quite clearly why more air in the didge gives more harmonics. The nearly pure sine wave present
at low pressure would correspond to the Fourier analysis of any "dull" sound, with few harmonic components. Then, as the pressure is
increased, the graph response becomes sharper, giving the "brighter" sound associated with a square wave or other harmonically rich,
straight waveforms. This is one part of what causes the didge's timbral modulation. (Fletcher, 1)
the
graph associated with the formula exhibits quite clearly why more air in the didge gives more harmonics. The nearly pure sine wave present
at low pressure would correspond to the Fourier analysis of any "dull" sound, with few harmonic components. Then, as the pressure is
increased, the graph response becomes sharper, giving the "brighter" sound associated with a square wave or other harmonically rich,
straight waveforms. This is one part of what causes the didge's timbral modulation. (Fletcher, 1)